Measuring user-perceived serendipity

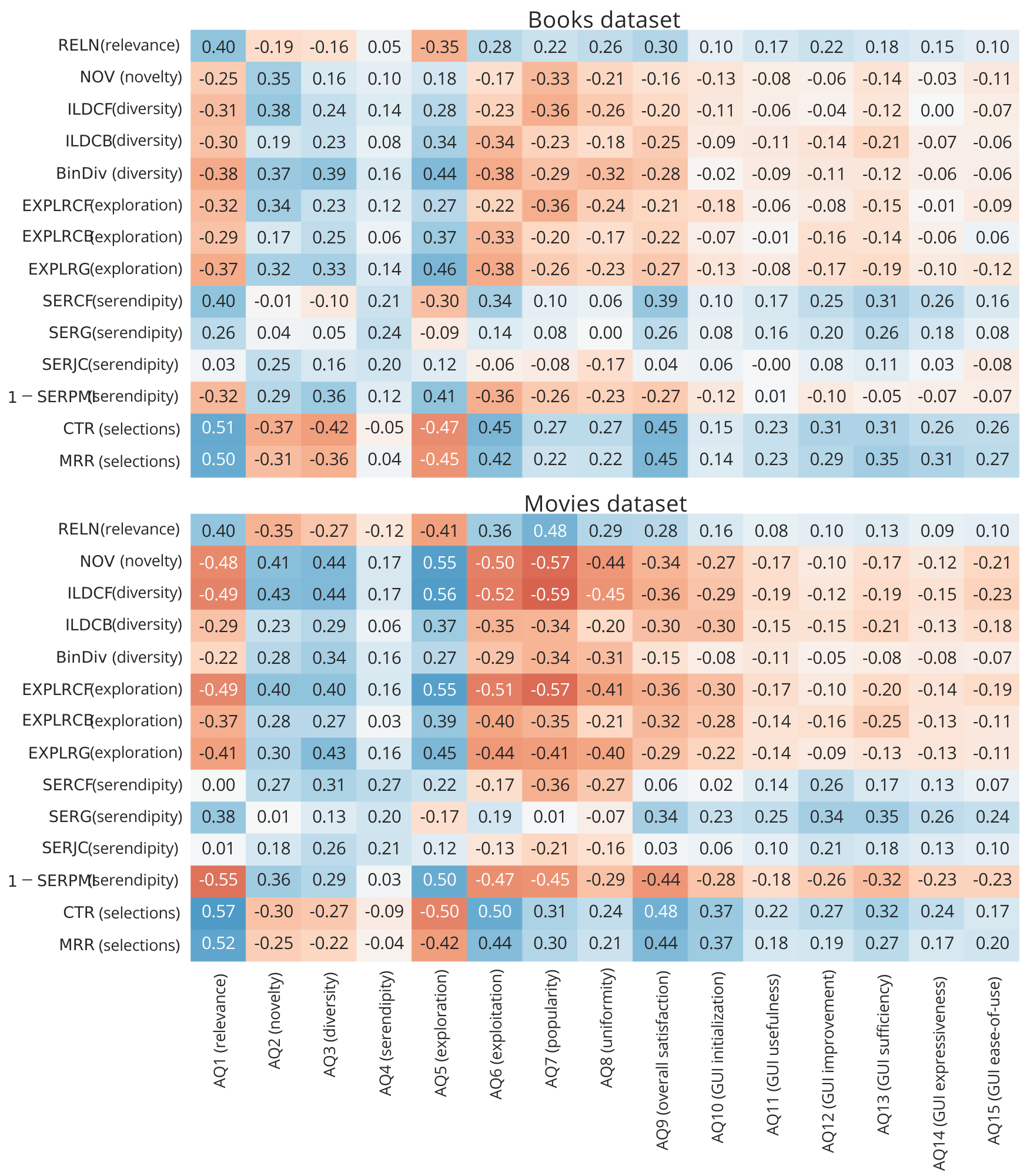
Your task would be to devise a metric, that would be capable of measuring (predicting, in case it will have a training part) to what extent were displayed results serendipitous from the user's perspective. Serendipity is one of the key concepts behind trully successfull recommendations, but on the other hand, it is notorously difficult to properly quantify.

At your disposal, there are results of a user study conducted on movie and book domains, where users were exposed to several iterations of recommendations (18 in total, supplied by 3 different algorithms). After each block of 6 iterations, users were asked to fill-in a questionnaire including their perception of recommendations serendipity. Your task is to use other available information (or collect some additional) to estimate this value.

Source data: https://osf.io/chbj9/?view_only=460e981414d349a3b667c254e3b5632d

Work-in-progress report: in the root folder. You probably only need to focus on sections 3,4 (study design and implemented algorithm variants), and eventually in the results on RQ2

Repository Content:

common folder

• common/df_books.csv, common/df_books.csv: mapping between internal IDs and those used in original datasets
• df_elicitation_selections.csv: selected items during the preference elicitation phase of the study (i.e., initial user profile)
• common/books.csv: additional metadata we collected for books (not directly used for results presentation)
• common/metadata_updated.json: additional metadata we collected for movies (not directly used for results presentation)

data folder

• distance_matrix_rating: the distance matrix of items w.r.t. cosine of their rating vectors (books and movies separately)
• item_item: trained EASE model with item-item relatedness (books and movies separately)

serendipity_task folder

• serendipity_task/after_block_questionnaire.json: results for questionnaire including serendipity evaluation
• serendipity_task/book_data_indexed_full.json: data used to present books*
• serendipity_task/movie_data_indexed_full.json: data used to present movies*
• serendipity_task/df_iteration_impressions_selections_serendipities.json: details about what users received and how they reacted

* not all information, but a substantial part:-)

import numpy as np
import pandas as pd
import json

C:\Users\lpesk\AppData\Roaming\Python\Python38\site-packages\pandas\core\computation\expressions.py:20: UserWarning: Pandas requires version '2.7.3' or newer of 'numexpr' (version '2.7.1' currently installed).
  from pandas.core.computation.check import NUMEXPR_INSTALLED

study_results = pd.read_json("serendipity_task/df_iteration_impressions_selections_serendipities.json")
questionnaire_results = pd.read_json("serendipity_task/after_block_questionnaire.json")

study_results["block"] = study_results["iteration"] // 6
study_results["block_iteration"] = study_results["iteration"] % 6

study_results.head(3)

#participation: ID of a user
#items: list of items displayed to the participant at this iteration
#selected_items = list of items the user selected at this iteration
#iteration: identification of the step in the study (0-17)
#   - the study was divided into 3 blocks (each served by a different algorithm), followed by the questionnaire
#   - block and block_iteration provide this information
#all other columns represent individual metrics evaluated on the full list of recommendations, or on the selected items ("sel" prefix)
#  - check the paper for metrics definitions

	index	participation	items	selected_items	iteration	cf_ild	cb_ild	bin_div	relevance	sel_cb_surprise	sel_cb_unexpectedness	sel_cf_unexpectedness	sel_incremental_genre_coverage	sel_pmi_unexpectedness	block	block_iteration
0	0	61	[1218, 4682, 745, 12886, 9719, 3416, 6387, 279...	[2796, 6387, 12886, 3416, 1723]	0	0.490715	0.533223	0.457035	18.308832	0.313333	0.723443	0.638649	0.0	0.205209	0	0
1	1	61	[10199, 12644, 1996, 9609, 11478, 12514, 9267,...	[9312, 9609, 5524, 10199, 7736]	1	0.658099	0.508626	0.328032	14.200634	0.190000	0.636354	0.662195	0.0	0.258737	0	1
2	2	61	[6707, 7784, 12259, 9072, 10906, 10193, 4648, ...	[12259, 1800, 3948, 10193, 10906]	2	0.587088	0.507497	0.238507	12.025384	0.073333	0.634591	0.625639	0.0	0.270986	0	2

questionnaire_results.head(5)
#dataset: which dataset the participant worked on
#participation: ID of the user
#block: to which block this questionnaire results correspond
#q1 - q9: responses to questions, 6-point Likert scale (strongly disagree = -3, somewhat agree = 1 etc.)
#   - nan correspond to "I dont understand" response
#   - q4 correspond to serendipity perception, i.e., this is your target value

	index	dataset	participation	block	q1	q2	q3	q4	q5	q6	q7	q8	q9
0	0	movies	61	0	1.0	-1.0	1.0	-1.0	-1.0	-1.0	1.0	1.0	1.0
1	389	movies	63	0	3.0	-1.0	2.0	3.0	1.0	-2.0	1.0	-2.0	3.0
2	1012	movies	61	1	-1.0	-3.0	-1.0	-1.0	2.0	-2.0	1.0	-1.0	-1.0
3	1370	movies	61	2	-1.0	1.0	1.0	-1.0	1.0	-1.0	1.0	1.0	1.0
4	1723	movies	63	1	2.0	1.0	-2.0	-2.0	-2.0	2.0	3.0	3.0	2.0

# list of all questions: 
# AQ1 relevance perception    The recommended movies matched my interests.
# AQ2 novelty perception      ... were mostly novel to me.
# AQ3 diversity perception    ... were highly different from each other.
# AQ4 serendipity perception  ... were unexpected yet interesting to me.
# AQ5 exploration perception  ... differed from my usual choices.
# AQ6 exploitation perception ... were mostly similar to what I usually watch.
# AQ7 popularity perception   ... mostly popular (i.e., blockbusters).
# AQ8 uniformity perception   ... mostly similar to each other.
# AQ9 overall satisfaction    Overall, I am satisfied with the recommended movies.

array([ 1.,  3., -1.,  2., -3., -2., nan])

Why is this a difficult task?

• we tried several common serendipity metrics; none of those provided a reasonable correlation with the user-perceived serendipity
• also no other evaluated metric was any better (we tried Pearsons correlation)

How to start?

• create some notion of item-to-item distance (or similarity)
  • we worked with rating vectors, genres, and plot embeddings; other alternatives are possible
• evaluate the difference between selected items and, e.g., so far known user profile
  • other alternatives possible, e.g., differences from the current offer, cluster analysis, uniqueness w.r.t. full user profile, ...
  • several ways to aggregate the differences (we only tried mean)
• aggregate results for all iterations of the block
  • we only tried mean values of the list-wise unexpectedness
• evaluate the correspondence with the user-supplied values
  • we only tried the Pearsons correlations of the whole dataset

Where to dig?

We tried several different notions of items similarity, so - although I believe there is still some space for further research, perhaps there are also other possible areas of interest, namely:

• How to aggregate the item-item similarity results (we only tried a simple mean with no weighting or no non-linearity whatsoever)
• Train your serendipity models if you devise some parameters that needs to be set
• Challenge the assumption of what serendipity mean. Check out some ideas of Brett Binst: https://www.serendipityengine.be/post/let-go-of-the-one-size-fits-all-definition-of-serendipity, https://dl.acm.org/doi/abs/10.1145/3640457.3688017
• Challenge how we evaluate the correspondence. Perhaps we already have good results per-user or per-[some other context], just do not consider them properly

What to always include?

• Reasons and hypotheses for the steps you performed: why do you think this is a good idea?
• Comparison with (some of the) existing methods (you already have their results)
• Results and conclusions: how do you read the obtained data?

How the semmestral work should look like?

There are multiple possible ways to tackle this problem. So, pick 2-3 promissing directions that sounds like fun to you and check them out (check them out = justify, code, evaluate, and analyze). Positive results are warmly wellcomed, yet the negative are expected (wellcome to the real world:-). Although, in case of negative results, I might ask you to go a few steps further to check few other options and so on.

Template code to start with:

# loading data
#item_item_movies = np.load("data/movieLens/item_item.npy")
item_item_books = np.load("data/goodbooks-10k/item_item.npy")

#distance_matrix_cf_movies = np.load("data/movieLens/distance_matrix_rating.npy")
distance_matrix_cf_books = np.load("data/goodbooks-10k/distance_matrix_rating.npy")

(item_item_books.shape, distance_matrix_cf_books.shape)

((6548, 6548), (6548, 6548))

• note that other pre-computed distance matrices can be found at https://osf.io/9y8gx/ in the "repro" folder

#unexpectedness of a single item
def item_unexpectedness(user_history, item, distance_matrix):
    return distance_matrix[user_history, item].mean()

#unexpectedness of a list of items, using collaborative distance matrix
def list_unexpectedness_cf(user_history, rec_list, dataset):
    if len(rec_list) == 0 or len(user_history) == 0:
        return 0    
    if dataset == "movies":
        return np.array([item_unexpectedness(user_history, x, distance_matrix_cf_movies) for x in rec_list]).mean()
    elif dataset == "books":
        return np.array([item_unexpectedness(user_history, x, distance_matrix_cf_books) for x in rec_list]).mean()


#usage in our codes:
# for i, row in df.iterrows():
#     full_hist = np.unique(elicitation_hist + iteration_hist)
#     df.loc[i, "sel_cf_unexpectedness"] = list_unexpectedness_cf(full_hist, curr_iter_selections, row.dataset)

#usage example
item_unexpectedness([1,5],6,distance_matrix_cf_books)

0.6519418720830903

#usage example
list_unexpectedness_cf([1,3,5,7], [2,4,6], "books")

0.5961706642294122

NEG_INF = -1e6

#estimated relevance of all items, using the knowledge of items previously selected by the user
def predict_scores(item_item, all_items, selected_items, filter_out_items, k=10):
    user_vector = np.zeros(shape=(all_items.size,), dtype=item_item.dtype)
    if selected_items.size == 0:
        return np.zeros_like(user_vector)
    user_vector[selected_items] = 1
    probs = np.dot(user_vector, item_item)
    # Here the NEG_INF used for masking must be STRICTLY smaller than probs predicted by the algorithms
    # So that the masking works properly
    assert NEG_INF < probs.min()
    # Mask out selected items
    probs[selected_items] = NEG_INF
    # Mask out items to be filtered
    probs[filter_out_items] = NEG_INF
    return probs

#usage example
all_books = pd.Series(range(0,item_item_books.shape[0]))
probs = predict_scores(item_item_books, all_books, pd.Series([6,7]), pd.Series([2]))
pd.Series(probs).describe()

count       6548.000000
mean        -458.154907
std        21402.509766
min     -1000000.000000
25%           -0.000657
50%            0.000003
75%            0.000671
max            0.246466
dtype: float64

from sklearn.preprocessing import QuantileTransformer

#normalization for the relevance scores; top-k here induces the indices of items (those recommended to the user)
def relevance_normed_movies(top_k, selected_items, filter_out_items):
    rel_scores = predict_scores(item_item_movies, all_movies, selected_items, filter_out_items, top_k.size)
    rel_scores_normed = QuantileTransformer().fit_transform(rel_scores.reshape(-1, 1)).reshape(rel_scores.shape)
    return rel_scores_normed[top_k].mean()#.sum()
    
#normalization for the relevance scores; top-k here induces the indices of items (those recommended to the user)    
def relevance_normed_books(top_k, selected_items, filter_out_items):
    rel_scores = predict_scores(item_item_books, all_books, selected_items, filter_out_items, top_k.size)
    rel_scores_normed = QuantileTransformer().fit_transform(rel_scores.reshape(-1, 1)).reshape(rel_scores.shape)
    return rel_scores_normed[top_k].mean()#.sum()

normed_scores = relevance_normed_books(pd.Series([1,4,9]),pd.Series([6,7]), pd.Series([2]))
normed_scores

0.9987033